Правильные выпуклые многогранники еще называют платоновыми телами. Великий древнегреческий философ Платон считал, что весь мир строится всего из четырех атомов — Огня, Земли, Воздуха и Воды, а каждый из этих атомов имеет форму одного из правильных многогранников — соответственно тетраэдра, куба, октаэдра и икосаэдра. Весь мир в целом, по Платону, построен в форме додекаэдра —пятого и последнего Платонова тела.

Платон думал о пространстве нашего мира, о его законах. И ему показалось, что он нашел неизменные первоосновы в бесконечно изменчивом мире. В самом деле, невозможно в нашем трехмерном пространстве придумать хотя бы еще один выпуклый многогранник, гранями которого служил бы правильный многоугольник, то есть фигура с равными сторонами и углами между ними. Таковы объективные пространственные законы.

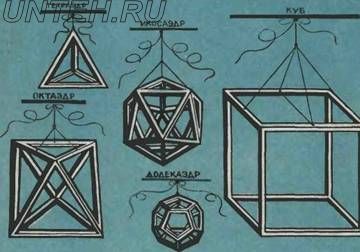
Платоновы тела, воспроизведенные художником с гравюр Леонардо да Винчи.

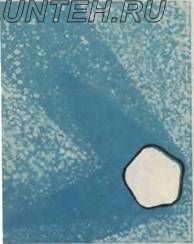
Вирус, снятый под электронным микроскопом.

Четыре равносторонних треугольника образуют правильную пирамиду — тетраэдр, восемь таких треугольников, соединившись, дают октаэдр, а двадцать — икосаэдр. Шесть квадратов объединяются в гексаэдр — всем нам известный куб. И наконец, двенадцать правильных пятиугольников образуют додекаэдр.

Но самая важная сторона жизни Платоновых тел связана с именами выдающихся ученых, с гениальными догадками, замечательными открытиями, изобретениями.

Иоганн Кеплер, открыв основные законы движения планет солнечной системы, не переставал размышлять: почему каждая из них находится именно на таком расстоянии от светила? Планет в его время было известно всего шесть, следовательно, расстояний между ними пять... Но и Платоновых тел тоже пять! Такое совпадение, подумал Кеплер, не может быть случайным. И он стал вставлять один правильный многогранник в другой, по-разному комбинируя их и вписывая каждый в сферу — математический прообраз планетных орбит. Построения эти обнаружили определенное сходство с небесным порядком, каким он виделся астрономам в те годы. Точные значения орбит у Кеплера, правда, не получились, и тогда он предположил, что есть разница между «мыслимой идеей круга и действительным путем планеты», поскольку «небесные движения — произведения не разума, а природы». Поэтому ему пришлось подправлять свою модель. Делать шары разной толщины. Скоро открыли новые планеты, запаса Платоновых тел не хватило, построения ученого рухнули. Однако именно в ходе этого геометрического эксперимента у Кеплера укрепилась поистине гениальная догадка, что орбиты планет — эллипсы!..

Платоновы тела долго оставались своеобразной игрушкой математиков. Но когда исследователи получили тончайшие инструменты для изучения глубин вещества, они оказались в центре внимания современных физиков, химиков, биологов. Известна была замечательная прочность, необыкновенная твердость кристаллов бора. Он наверняка мог сгодиться для обработки самых твердых сплавов. Крепость и твердость бора и прежде связывали с особым строением кристаллической решетки. И вот, когда ее сумели расшифровать, оказалось, что каждая элементарная ячейка кристалла представляет собой икосаэдр! В двенадцати вершинах этой фигуры расположено по атому бора. Максимальная плотность, компактность такого каркаса, равная прочность во всех его правильных гранях немало служат замечательным свойствам бора. Чтобы вырвать хотя бы один атом бора, нужно «потревожить» всю предельно жесткую и плотную конструкцию.

Это свойство равной прочности, жесткости во всех гранях используют, кстати, в пакетах молока, в форме тетраэдра. Кроме того, они очень экономно укладываются, занимая минимум места.

Причиной восхищения ученых послужило еще одно удивительное достоинство Платоновых тел. Речь идет об их свойстве ограничивать собой самый большой объем из всех возможных фигур с тем же числом сторон. Пример его использования открыли в живой природе, когда исследователи решили уточнить форму «сферических вирусов». Для этого вирус с разных сторон сфотографировали под электронным микроскопом. Тень от вируса имела... острые углы! Значит, вирус вовсе не круглый, как считали раньше?! Тогда принялись фотографировать различные многогранники. Оказалось, лишь икосаэдр дает тень такую же, как вирус.

Почему же именно икосаэдр? Лауреат Нобелевской премии Джон Кендрью дает такой ответ. «По-видимому, тут все дело в экономии — экономии генетической информации. Вирусная частица должна весь обмен клетки-хозяина перевернуть вверх дном; она должна заставить зараженную клетку синтезировать многочисленные ферменты и другие молекулы, необходимые для синтеза новых вирусных частиц. Все эти ферменты должны быть закодированы в вирусной нуклеиновой кислоте. Но количество ее ограничено Поэтому для кодирования белков собственной оболочки в нуклеиновой кислоте вируса оставлено совсем мало места. Что же делает вирус? Он просто использует много раз один и тот же участок нуклеиновой кислоты (точь-в-точь, как архитекторы используют одинаковые стержни. — Прим. ред.) для синтеза большого числа стандартных молекул — строительных блоков, объединяющихся в процессе самосборки вирусной частицы. В результате достигается максимальная экономия генетической информации. Остается добавить, что по законам математики для построения наиболее экономичным способом мкнутой оболочки из одинаковых элементов нужно сложить из них икосаэдр, который мы наблюдаем у вирусов».

Этим свойством икосаэдра и хотят воспользоваться архитекторы, чтобы на выпуклом экране гелиоустановки уместилось максимальное число плоских треугольников-фотоэлементов.

К. ЛЕВИТИН

Рисунки В. БУТУРЛИНЦЕВА