Популярное

Язык машины

Помните удивительную историю с пляшущими человечками, рассказанную знаменитым Шерлоком Холмсом своему другу доктору Ватсону? Помните странные записки, которые преступник посылал своей жертве? На них были нарисованы целые хороводы пляшущих фигурок, вроде нарисованных внизу на этой странице.

«Что в них особенного, детские рисунки, глупая забава!» — подумает всякий. А вот Шерлок Холмс, хорошо знакомый с различными видами тайнописи, сразу определил: перед ним шифр. Он понял, что фигурки означают буквы, и начал искать ключ.

Найдя его знаменитый сыщик не только прочел все записки, но и сам послал преступнику короткое послание.
И... преступник попал в руки правосудия. Пляшущие фигурки означили слова: «Приди сюда немедленно».
Существует много систем тайнописи. Вот одна из них.

Что написано на клочке бумаги, нарисованном на стр. 54? Вы просидите над шифром годы, перепробуете миллиарды комбинаций, — не знаете ключа, не прочтете! А между тем, владея им, узнать содержание зашифрованного текста не составляет особого труда.
Возьмите листок бумаги и вырежьте в нем отверстия точно по рисунку. Получится решетка. Наложите ее цифрой 1 вверх на беспорядочно написанные буквы квадрата. В отверстиях появится текст: «электронная вычис...» Поверните решетку по часовой стрелке на четверть оборота, потом еще и еще раз. Вы прочтете всю фразу.

Подсчитано, что 16 окошек, необходимых для кодирования, можно набрать невероятно большим числом способов — более чем четырьмя миллиардами. Разгадать такой шифр можно, только имея решетку. Чтобы она случайно не попала в чужие руки, придумали способ хранения решетки в памяти. Вот тут-то и помогла математика.

Проставим в клетках нашей решетки, там, где нет выреза, ноли, а в вырезах — единицы.

Мы получим восемь рядов цифр (см. рисунок на стр. 55 вверху). Запомнить расположение такого большого количества Цифр довольно трудно. Но математики нашли здесь интересную закономерность и максимально упростили задачу. Как они это сделали, станет понятно после знакомства с другими способами кодирования.

Шерлок Холмс, как вы помните, имел дело со множеством символов — с пляшущими человечками. Существовали системы тайнописи с шифровкой группы букв, с кодированием самой решетки только с помощью двух символов.

А нельзя ли двумя символами кодировать и текст?

Вот ряд условных знаков: только точки и тире. Что они означают? (рис. на стр. 55 внизу).

Если вы знаете азбуку Морзе, то прочтете ту самую фразу, что расшифровали с помощью решетки. Значит, весь алфавит можно закодировать, комбинируя только два знака.

Это очень удобно для кодирования. Можно каждый знак передавать или записывать с помощью электрического тока. Например, меняя его продолжительность (точка, тире), или направление (плюс, минус), или амплитуду — есть сигнал, нет сигнала (единица, ноль). Последний способ применяется в электронных счетных машинах, потому что в машине надежнее всего различаются отсутствие и появление сигнала.

Если вы внимательно рассматривали азбуку Морзе, то заметили, вероятно, что некоторые буквы передаются одним-двумя знаками (Е — точкой, Т— тире, А — точкой и тире, И — двумя точками и т. д.), а другие четырьмя и даже пятью (Ш — четыре тире, X — четыре точки, Ч — три тире, точка, Э — две точки, тире, две точки).

Вначале возьмем только два знака. Получим:

А = 00 В=10
Б = 01 Г=11

22 — 4 — на этом наши возможности исчерпались. Возьмем три знака:

А = 000 Д = 100
Б = 001 Е = 101
В = 010 Ж= 110
Г = 011 3 — 111

И опять подошли к пределу — 2.ч — 8.

Мало будет и четырех знаков — ТА = 16. Только пять знаков дадут нужный нам результат — 25 — 32, как раз то число комбинаций, которое необходимо для кодирования букв русского алфавита.

Составим такой код, где буквы будут иметь вид:

А= 00000 Б 00001 В = 00010 Г = 00011

д= 00100 Е = 00101  ж =  00110 3 = 00111 И = 01000...

Буква «Н» изобразится как 01100, «Ч» — 10110 и «Я» — как 11011.
Из скольких знаков должна состоять кодовая группа, чтобы записать все цифры от 0 до 9 тоже одинаковым количеством нолей и единиц? И здесь, оказывается, двух и трех знаков мало. А вот четырех достаточно. Они дают шестнадцать комбинаций — 21, а нам надо всего десять.
Вот как будут выглядеть цифры кодированном виде:

0 = 0000 1 = 0001 2 = 0010 3 = 0011 4=0100  5 = 0101 6 = 0110 7 = 0111 8 = 1000  9=1001

Но не подумайте, что эти коды алфавита и цифр единственные. Их может быть очень много. Воспользуемся нашими кодами и закодируем такое слово, как «кибернетика» и число 13.

Слово будет выглядеть как группы нолей и единиц.

(01001) (01000) (00001) (00101) (10000) (01100) (00101) (10010) (01000) (01001) (00000)
Число 13 запишется как (0001) (0011).

Для записи двухзначного числа понадобилось восемь знаков. Это много. А можно ли обойтись меньшим количеством знаков? Можно. Для этого нужно изобразить число с помощью тех же 0 и 1 не кодовыми группами, а в двоичной системе счисления.
Мы привыкли к так называемому десятичному счислению, по которому все числа разделены на единицы, десятки, сотни, тысячи. Но есть и другие системы счисления.
От древних народов мы унаследовали, например, двенадцатеричную систему и по ней ведем счет часам и месяцам.

В Англии дюжинами ведут счет в торговле, а расплачиваются по сложной денежной системе, в которой за единицу принят один пенс.

Двенадцать пенсов — это один шиллинг, а двадцать шиллингов — один фунт.

Индейцы племени майя применяли оригинальную четвертично-пятеричную систему. Они пользовались нолем, называвшимся у них «раковиной», для образования 20, 40 и т. д. Число изображалось полосками и точками, причем полоски соответствовали числу рук и ног, которыми пользовались при счете, а точки — количеству пальцев на руке или ноге.

Знаменитый русский ученый и путешественник Миклухо-Маклай, наблюдавший жизнь туземцев Новой Гвинеи, писал:

«Излюбленный способ счета состоит в том, что папуас загибает один за другим пальцы руки, причем например «бе, бе, бе...». Досчитав до Затем он загибает пальцы другой руки, снова повторяет «бе, бе...»,л с пока не доходит до «ибон-али» (две руки). Затем он идет дальше, приговаривая «бе, бе...», пока не доходит до «самба-бе» и «самба-али»)J (одна нога, две ноги). Если нужно считать дальше, папуас пользуется^, пальцами рук и ног кого-нибуд другого».

Существует и двоичное счисление. Оно-то и служит «языком» машины. В нем есть всего два символа: ноль и единица.
В отличие от десятичной системы, где за основание числа берется величина 10 и в каждом разряде может быть десять цифр — от 0 до 9, здесь за основание числа берется величина 2. Каждый разряд имеет две цифры: 0 или 1, и каждый следующий разряд больше предыдущего в два раза.

Таким способом мы кодировали отверстия решетки шифра.

Вот столбик чисел (стр. 57 слева). Если считать, что это обычная десятичная запись, то единица следующего разряда в десять раз больше единицы предыдущего. Если же принять запись по двоичной системе, то единица, стоящая на последнем, самом правом, месте, тоже обычная единица, но единица следующего разряда — на втором месте справа — уже не в десять раз больше ее, а только в два и означает двойку, а третья единица — четверку, четвертая — восьмерку, пятая — шестнадцать и т. д.

Желая записать какое-нибудь число, например одна тысяча семнадцать, по десятичной системе, мы разлагаем его на составные части, соответствующие разрядам этой системы, а затем уже производим запись: тысяч — одна( ставим единицу в разряде тысяч), сотни отсутствуют (ставив ноль в разряде сотен), десятков — один (ставим единицу в разряде десятков), единиц — семь (ставим семерку в разряде единиц). Получается запись 1017.

При записи какого-либо числа по двоичной системе мы так же разлагаем его на разряды, но разряды здесь будут иные — следовательно, и запись иная. Так, в числе 7 четверок — одна, двоек — одна, единиц — одна (7 = 4 + 2 + 1 = 2²+2¹+2⁰) — следовательно, в каждом из этих разрядов ставим по единице, получается 111. Так же поступаем и с другими числами.

Теперь вы, вероятно, догадываетесь, что для шифрования рядов нашей решетки надо представить себе, что они написаны в двоичной системе и перевести в десятичную. Тогда первый ряд решетки — 01010010 превратится в 82, А для расшифровки нужно произвести обратную операцию и там, где будут стоять единицы, вырезать окошки в решетке.

Понятно, что ряд чисел в десятичной системе для нашей решетки запомнить будет не так трудно. Одно дело, скажет каждый, заниматься шифрованием и писать ноли и единицы на бумаге, а совсем другое — в машине. Как машина справляется с записью чисел?

Каждый видел нехитрое устройство на садовых калитках: небольшая деревяшка свободно вращается на вбитом в ее середину гвозде. У такой вертушки может быть только два положения: она может либо закрыть дверь. либо открыть. Среднего положения у нее не бывает. Кроме того, вертушка может как угодно долго быть закрыта или открыта.

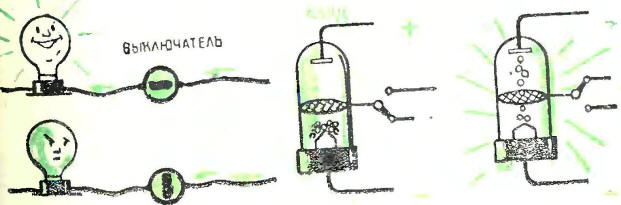
Вертушку напоминает кнопочный выключатель настольной лампы. Выключатель может -быть либо включен, либо выключен. Среднего положения у него тоже не бывает. Причем выключатель будет находиться в одном из этих положений, пока мы, нажав пальцем кнопку, не переведем его в другое. Другими словами, он неограниченно долго может зафиксировать — «запомнить» включена или выключена лампа.
По такому же принципу работают своеобразные реле, так называемые триггеры, с помощью которых в электронных вычислительных машинах ведется запись и счет чисел.

Упрощенно триггер можно представить в виде двух электронных ламп, смонтированных в одной колбе.
Вы, конечно, знаете, что при включении лампы катод разогревается и с него к аноду устремляется поток электронов.
Электричеством управляют с помощью электричества. На пути электронов, между катодом и анодом, поставлен еще один электрод — сетка — регулировщик движения электронов. Если на сетку подать достаточно большое отрицательное напряжение, то поток электронов остановится — лампа выключится. При положительном заряде на сетке электроны снова начнут проскакивать через нее — лампа включится.

В триггере две такие лампы составляют единое целое. Электрически они соединены так, что если первая лампа включена, то вторая обязательно будет выключена, и наоборот. Одно из таких устойчивых состояний триггера кодируется как 1, а другое — как 0.
Каждый новый электрический импульс, подаваемый на сетки ламп, поочередно то пропускает поток электронов в одной из них, то останавливает его. И триггер в точном соответствии с поступившим импульсом меняет свое состояние, показывая то единицу, то
ноль.

В любом из двух состояний триггер, подобно выключателю, может пребывать сколь угодно долго, пока не поступит новый импульс. Следовательно, триггер может хранить, «помнить» 1 или 0 до тех пор, пока это нужно, пока не поступит новый сигнал. Так, триггер, переходя из одного состояния в другое, или, как говорят иногда, «опрокидываясь», позволяет отмечать импульсы.

Механическое устройство — вертушку — мы можем повернуть за 1/2 секунды, электрическое устройство—выключатель — срабатывает уже за 1/300 секунды, а «опрокидывание» триггеров благодаря особенностям электронных ламп происходит с невероятной, колоссальной быстротой — за 1/1000000 долю секунды, В этом и заключается один из секретов быстроты счета электронной машины. Триггеры собирают в триггерные цепи — счетчики.

Вот перед нами четыре триггера, соединенных в цепь. У каждого из них по два входных и выходных контакта. Перед началом счета на всех триггерах зафиксировано состояние ноль, то есть цепь-счетчик показывает 0000 (см. стр. 58 вверху).

Теперь представим, что на входные контакты первого слева триггера подан электрический сигнал — импульс. Тогда первый триггер «опрокинется» и покажет 1, а на остальных все так же будет 0. Следовательно, цепь покажет 0001.

Подадим теперь второй импульс. Первый триггер выключится (опять даст 0) и передаст импульс на следующий триггер. На нем зафиксируется единица. Цепь покажет 0010.

Такую систему триггеров можно сравнить со счетами, на каждой палочке у которых всего по две костяшки. Для ведения на них счета, подобно тому как и на обычных счетах, необходимо соблюдать одно правило: когда все костяшки данной палочки «израсходованы» передвинуты справа налево, надо передвинуть одну костяшку на следующей палочке, а костяшки на нижней вернуть в исходное положение.
Итак, даем третий импульс. Он снова включит первый триггер, а остальные не изменят своих положений. Цепь покажет 0011.

Продолжая наши рассуждения, получим для пятого импульса 0101, для шестого — 0110, для седьмого — 0111, для восьмого — 1000... для пятнадцатого — 1111.

Запись чисел с помощью триггеров можно произвести и в десятичной системе счисления, как мы это делали, когда записывали число 13.
Видно, что сравнение не в пользу последнего способа — требуется больше триггеров: там четыре, а здесь восемь.
И, несмотря на это, в машинах таким способом тоже пользуются. Между прочим, подумав, вы догадаетесь, как триггеры могут записывать и слова.

Итак, цепь триггеров фиксирует и считает. На первый взгляд может показаться, что для подсчета больших чисел необходимо огромное количество триггерных ячеек. Здесь уместно вспомнить индийскую легенду о том, как царь Шерам предложил мудрецу Сете — изобретателю шахмат — самому себе определить награду за великолепную игру. Тогда Сета положил перед царем шахматную доску и попросил, чтобы в каждую из ее 64 клеток положили пшеничные зерна, причем в первую клеточку 1, во вторую 2, в третью 4, и так в каждую последующую ровно вдвое больше, чем в предыдущую. Желание мудреца показалось очень скромным, однако своей награды он так и не получил. Математики царя Шерама подсчитали, что количество зерен выражается не поддающимся воображению гигантским числом — восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать. Это зерно заполнило бы гигантский амбар длиной от Земли до Солнца.

А ведь изобретатель шахмат сумел это число получить с помощью лишь 64 клеток. Так и в современных электронных вычислительных машинах цепочка всего из 64 триггеров способна пересчитать огромное «шахматное число».

Вот как удивительны возможности электронных счетчиков современных электронных вычислительных машин.