Новая головоломка Рубика

• Пб для школы вода и геометрия
• Электронная ударная установка
• Молекула-гантель
• Скачать ЮТ №8 1981 год
• Вариатор и пневматика

(см. «ЮТ» № 7 за 1982 год и № 2 за 1983 год}, Рубик продолжает работать над новыми головоломками.

Последнее свое изобретение он назвал «волшебная змея». В эту головоломку с удовольствием будут играть и те, для кого кубик Рубина оказался слишком сложным. Дело в том, что в отличие от кубика змея не имеет единственного, заранее известного решения. Изменяя ее форму, можно получить множество разнообразных фигур. Математики подсчитали, что их количество равно колоссальному числу: 90 квадриллионам (2 • 1016}. Задача играющего состоит в том, чтобы найти самые интересные и самые сложные из них.

У новой головоломки есть еще одно достоинство: ее легко сделать самому. Об этом мы вам расскажем и продемонстрируем примеры фигур, которые можно сложить из змеи.

КАК СДЕЛАТЬ ВОЛШЕБНУЮ ЗМЕЮ

Змея Рубика состоит из 24 одинаковых равнобедренных треугольных призм, последовательно соединенных между собой серединами боковых граней. Это соединение подвижно: каждь и эле мент змеи вращается относительно соседних.

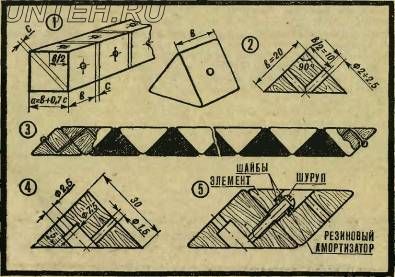
Посмотрите на рис. 1. Элементы змеи выпиливают из деревянного бруска квадратного сечения. Совсем необязательно искать брусок, в точности соответствующий размерам, приведенным на чертежах. Брусок может быть чуть тоньше или чуть толще, но в этом случае вам придется пересчитать размеры элементов в соответствии с формулами на том же рисунке. Обозначения: а — ширина бруска, в — размер боковой грани элемента, с — ширина пропила, зависящая от развода зубьев вашей пилы.

Прежде чем распилить брусок на заготовки для элементов, в нем сверлят сквозные взаимно перпендикулярные отверстия 01,5— 2 5 мм. Затем брусок распиливают сначала вдоль оси по диагонали сечения, а затем поперек на отдельные* элементы. В результате получится 24 заготовки, одна из которых показана на рисунке 2. Остается аккуратно зачистить их напильником и шкуркой, а затем покрасить. Половина элементов должна быть покрашена в один цвет, половина — в другой. При сборке цвета чередуются.

Дальше можно пойти одним из двух путей. Если, ваш исходный брусок имеет сечение менее 25 X 25 мм, змею удобнее всего собрать, протянув через внутренние каналы всех 24 элементов прочную резинку. На концах змеи резинку следует привязать к металлическим колечкам — они не дадут ‘ ей выскочить. Змея готова (рис. 3).

Если же размеры сечения бруска превышают 25X25 мм, имеет смысл сделать крепление чуть сложнее, зато прочнее: соединить элементы шурупами. Элемент головоломки, предназначенный для соединения таким способом, изображен на рис. 4. Диаметр шурупов 2—3 мм, длина 15—25 мм, в зависимости от размеров элементов. Под головки шурупов подложите шайбы, а под них — резиновые амортизаторы толщиной 2—4 мм. Их можно заменить пружинками в 2— 3 витка из тонкой стальной проволоки. Как соединить элементы между собой, показано на рис. 5.

КАК ИГРАТЬ С ВОЛШЕБНОЙ ЗМЕЕЙ

Попробуйте сложить из вашей змеи какие-нибудь замысловатые фигуры, поворачивая соединенные элементы ее тела относительно друг друга. Предвидим: вначале змея может показаться вам очень простой игрушкой, несравненно проще кубика Рубика. Но не спешите. После первых успехов выяснится, что сложить из змеи красивую симметричную фигуру не так просто. К тому же волшебная * змея изобретена сравнительно недавно и поэтому хранит еще немало тайн, даже от опытных знатоков головоломок.

На наших рисунках приведено лишь несколько из двух квадриллионов возможных фигур. Каждая из них является многогранником с определенным числом граней. Теоретически количество граней у фигур, сложенных из волшебной змеи, может колебаться от 6 до 38. Но… пока еще

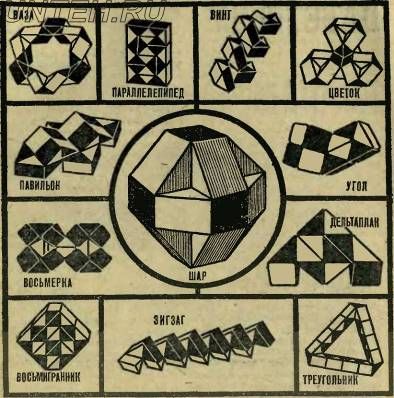
неизвестно, любые ли многогранники можно из нее получить. Например, можно ли сложить 9-, 11-, 15-граннйки?.. Это пока никому нз удалось, впрочем, никому не удалось и доказать, что это невозможно.

Есть еще одно направление изобретательского творчества, связанное с волшебной змеей. Ведь элементам змеи вовсе не обязательно иметь форму треугольных призм. А что, если их заменить другими многогранниками? Кроме того, одна змея может состоять из неодинаковых по форме элементов… Словом, змея Рубика — настоящее «белое пятно» на карте головоломок.

А. КАЛИНИН Рисунки С. ЗАВАЛОВА

Ют №6 1984 год |