Подробности для любознательных. Живые счеты

• О проекте
• Игрушки изучают инженеры
• Работа для солнца
• Электрофонная точность
• Проектирование по… Летописям

Расчетные задачи возникали еще в каменном веке. Уже тогда первобытным людям волей-неволей приходилось считать, скажем, сколько каменных топоров нужно отдать за шкуру мамонта или, например, сколько воинов должно выставить племя для обороны от соседей. Самым естественным помощником в таких вычислениях были пальцы. Чтобы убедиться в этом, совсем не обязательно путешествовать в глубь веков. Всего лишь сто лет назад туземные племена Новой Гвинеи жили первобытной общиной.

Известный русский путешественник Миклухо-Маклай свидетельствовал: при счете папуас загибает один за другим пальцы руки. При этом он издает определенный звук, например -«бе-бебе». Досчитав до пяти, папуас произносит «ибон-бе» (рука). Затем загибает пальцы другой руки, повторяя свое «бе-бе», пока не доходит до «ибон-али» (две руки). Затем идет дальше, до «самоа-бе» и «самба-али» (одна нога, две ноги). Нетрудно догадаться, что при крупных «торговых операциях» первобытным людям приходилось использовать руки и ноги соплеменников.

УМНОЖЕНИЕ ПО-ЕГИПЕТСКИ

Складывать и вычитать в египетской системе было легко, но,

чтобы научиться делить и умножать, нужно было обладать чуть ли не «высшим» образованием. Решим по-египетски один такой пример. Предположим, нам нужно перемножить 13 и 29. Для этого египтяне выписали бы на нашем месте рядом 1 и 29. Затем последовательно начали бы удваивать эти числа, выписывая результат в столбик. /1   29

2        58

/4       116

/8       232

Удвоение продолжали до тех пор, пока из чисел левого столбца не удавалось составить в сумме второй сомножитель. В нашем случае число тринадцать можно составить из 1, 4, 8. Соответствующие строки египтяне отмечали черточками и числа правого столбца в этих строках складывали. 29+116-1-232=377. Как видите, система счета довольно громоздка.

ДО ДЕСЯТИ — УДОБНЕЕ

Привычная и удобная десятичная система была создана в Индии, а затем заимствована арабами. В IX веке математик Мухаммед аль-Хорезми написал трактат о десятичной системе и вычислениях в ней. В XII веке с латинским переводом этого трактата познакомилась Европа. Благодаря трудам аль-Хорезми и других арабских математиков десятичная система получила повсеместное распространение, вытеснив громоздкие и неудобные египетскую и римскую.

глазах. А как считает микрокалькулятор? Как он мгновенно складывает, умножает, делит?

Начнем с того, что «мозг» калькулятора — большая интегральная схема. Она не воспринимает привычную нам запись чисел, а работает лишь с двумя — нулем и единицей. Поэтому специальный узел микрокалькулятора, соединенный с клавиатурой, переводит числа из десятичной системы в понятный машине код, где каждая цифра представляется в двоичной системе. Вот так выглядят в этом коде цифры от нуля до девяти.

АБАК, СЧЕТЫ И ПАСКАЛЬ

Трудоемкость вычислений заставила изобретать вычислительные устройства. Уже в Древней Греции и Риме был известен абак — доска с углублениями, в которые клали камешки. В зависимости от положения камешки изображали разные числа; в русских счетах роль камешков выполняют костяшки. Счеты удобнее абака, но и на них считать не очень удобно.

В 1642 году юный математик Блез Паскаль (ему не было тогда и двадцати) выдвинул идею машины, выполняющей арифметические действия способом «столь новым, сколь и удобным». Машина Паскаля состояла из сложной системы зубчатых колес. Начиналась история вычислительных машин…

ТАКОЕ СЛОЖНОЕ СЛОЖЕНИЕ

Действия на счетах, вычисления на бумаге наглядны — все на

0	0000	5	0101
1	0001	6	0110
2	0010	7	0111
3	ООН	8	1000
4	0100	9	1001

Правила, по которым микро калькулятор оперирует с числами, тоже особые. Расскажем, к примеру, о сложении. Предположим, нам нужно сложить 5 и 7. В двоичном коде, напомним, 5 записывается как 0101, 7—0111. При сложении 0 и 1 в сумме получается 1, при сложении 1 и 1 в сумме получается 0, а 1 переносится в старший разряд. Пользуясь этими правилами, проведем сложение.

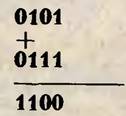
КАКОЙ ВЫБРАТЬ КАЛЬКУЛЯТОР?

По-видимому, этот вопрос волнует многих. На витринах магазинов выставлено много различных моделей. На какой же остановить выбор? Постараемся дать некоторые рекомендации.

Самая простая и дешевая модель — «Электроника Б3-23» (цена 25 рублей). Рекомендовать ее можно лишь младшим школьникам. Уж слишком ограничен круг ее операций — четыре действия арифметики да вычисление процентов. Вот и все. Кроме того, эта модель не имеет памяти, и промежуточные результаты придется записывать на бумаге.

Более совершенна «Электроника БЗ-26» (цена 35 рублей). Она запоминает промежуточные результаты и извлекает квадратные корни.

Обе эти модели (и подобные им) можно использовать для наших занятий, но, когда нам понадобится вычислять синусы или косинусы углов, придется обращаться к таблицам или логарифмической линейке.

Пожалуй, наиболее отвечает нашим целям микрокалькулятор «Электроника Б3-37», знакомый и с тригонометрией и с логарифмами. Цена его — 50 рублей. Это немало. Но ведь микрокалькулятор покупают не на один год. Такая совершенная модель пригодится вам и в старших классах, и в институте, и на работе.

лю в регистрах калькулятора соответствуют всего два состояния: включен — выключен. И, несмотря на сложность, вычисления происходят очень быстро. Например, для сложения двух шестизначных чисел микрокалькулятору нужны всего полторы десятитысячные доли секунды.

Рисунки Е. ВИНОДАРОВОИ

!Без Категории, ЮТ №1 1985 год |